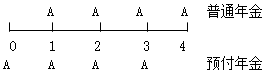
(1)預付年金(即付年金、期初年金):從第一期起,各期期初收付的年金

①n期內共發生n筆年金(n個A);
②第1筆年金發生在時點0(第一期期初),最后1筆年金發生在時點n-1(最后一期期初)。
【提示】
在期數相同的情況下,普通年金與預付年金的年金個數相同(n期內有n筆年金);二者的區別僅在于收付款時間的不同:普通年金發生于各期期末(1~n),在0時點(第一期期初)沒有發生額;預付年金發生于各期期初(0~n-1),在n時點(最后一期期末)沒有發生額。
(2)預付年金終值:由于預付年金的每一筆年金都比普通年金提前一期發生,因而在計算終值時,預付年金的每一筆年金都要比普通年金多一個計息期。

預付年金終值=普通年金終值×(1+i)

=A×[(F/A,i,n+1)-1]
即:預付年金終值系數是在普通年金終值系數基礎上,期數加1,系數減1的結果。
【示例】
某公司打算購買一臺設備,付款方式為每年初支付200萬元,3年付訖。假設年利率為5%,復利計息。則該公司購置設備的付款額終值為:
F=200×(F/A,5%,3)×(1+5%)=200×[(F/A,5%,4)-1]=662.02(萬元)
(3)預付年金現值:由于預付年金的每一筆年金都比普通年金提前一期發生,因而在計算現值時,預付年金的每一筆年金都要比普通年金少折現一期。

預付年金現值=普通年金現值×(1+i)
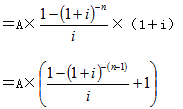
=A×[(P/A,i,n-1)+1 ]
即:預付年金現值系數是在普通年金現值系數基礎上,期數減1,系數加1的結果。
(責任編輯:)